Comprendre l’impédance
L’impédance est une mesure de la résistance d’un circuit au passage du courant lorsqu’une tension est appliquée. C’est un concept clé dans la conception et la compréhension des circuits. Que vous travailliez sur un grand projet industriel ou sur un petit kit électronique DIY, savoir comment calculer l’impédance vous aidera à améliorer le fonctionnement de vos appareils et à éviter les problèmes.
Dans ce guide ultime, nous allons explorer en profondeur comment trouver l’impédance dans un circuit. Nous allons décomposer cela étape par étape, vous fournir toutes les formules et exemples dont vous avez besoin, et même ajouter des images et tableaux utiles pour vous assurer de bien comprendre.
Quelle est la règle pour l’impédance dans un circuit ?
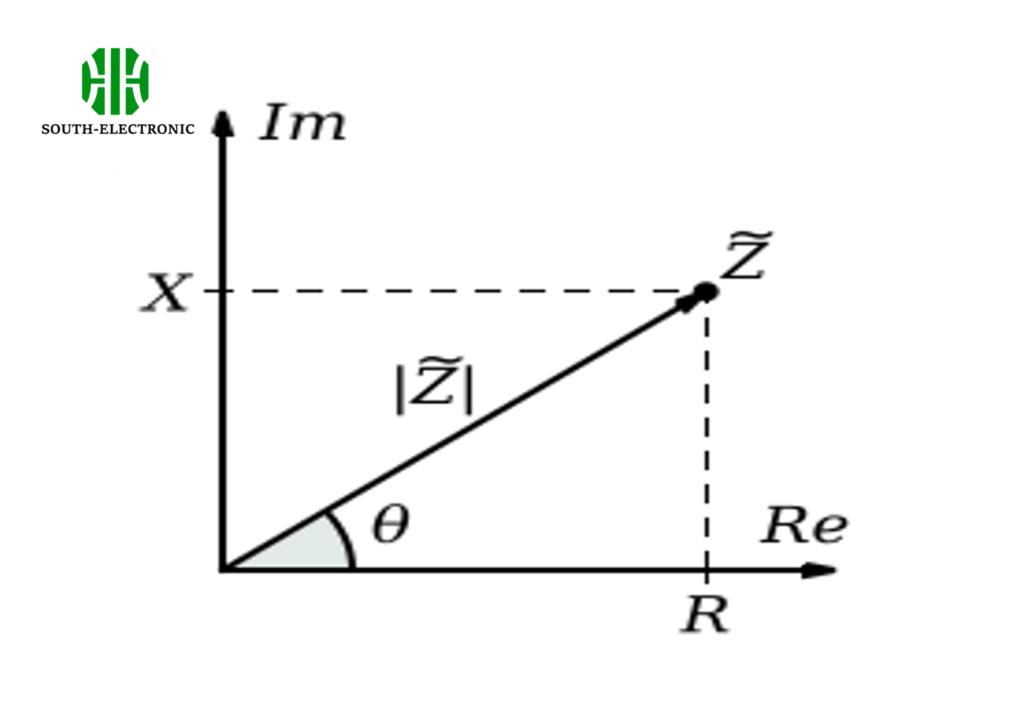
L’impédance (Z) dans un circuit est la somme vectorielle de la résistance (R) et de la réactance (X). La formule est donnée par :
Z=R2+X2Z = \sqrt{R^2 + X^2}Z=R2+X2
- Résistance (R) : L’opposition au courant continu (DC).
- Réactance (X) : L’opposition au courant alternatif (AC), qui peut être inductive (X<sub>L</sub>) ou capacitive (X<sub>C</sub>).
Pour une inductance :
XL=ωLX_L = \omega LXL
où ω=2πf\omega = 2\pi fω=2πf (fréquence angulaire), et L est l’inductance.
Pour un condensateur :
XC=1ωCX_C = \frac{1}{\omega C}XC
où C est la capacité.

Comment vérifier l’impédance d’un fil ?
L’impédance d’un fil peut être mesurée en utilisant la méthode courant-tension (I-V). Cela implique d’appliquer une tension connue au circuit et de mesurer le courant résultant. La formule utilisée est :
Z=VIZ = \frac{V}{I}Z=IV
Étapes :
- Appliquer une tension connue (V) à travers le fil.
- Mesurer le courant (I) passant à travers le fil.
- Calculer l’impédance en utilisant la formule ci-dessus.
Exemple de mesures de la méthode I-V
| Tension (V) | Courant (I) | Impédance (Z) |
|---|---|---|
| 5V | 0.5A | 10Ω |
| 10V | 1A | 10Ω |
| 15V | 1.5A | 10Ω |

Quels facteurs déterminent l’impédance ?
L’impédance est déterminée par plusieurs facteurs :
- Résistance : La résistance inhérente des composants et des matériaux dans le circuit.
- Réactance inductive : Causée par les inductances dans le circuit.
- Réactance capacitive : Causée par les condensateurs dans le circuit.
- Fréquence du signal AC : Des fréquences plus élevées augmentent la réactance inductive et diminuent la réactance capacitive.

Comment trouver l’impédance dans un circuit parallèle ?
Trouver l’impédance dans un circuit parallèle implique de calculer l’impédance totale à partir des impédances de chaque branche. La formule est :
1Ztotal=1Z1+1Z2+⋯+1Zn\frac{1}{Z_{\text{total}}} = \frac{1}{Z_1} + \frac{1}{Z_2} + \cdots + \frac{1}{Z_n}Ztotal
Étapes :
- Calculer l’impédance de chaque branche.
- Utiliser la formule ci-dessus pour trouver l’impédance totale.
Exemple d’impédance dans un circuit parallèle
| Branche | Impédance (Z) |
|---|---|
| Z1 | 20Ω |
| Z2 | 30Ω |
| Z3 | 60Ω |
| Total | 10Ω |
Comment calculer l’impédance dans un circuit AC ?
L’impédance dans un circuit AC est calculée en utilisant à la fois la résistance et la réactance. L’impédance totale est :
Z=R2+(XL−XC)2Z = \sqrt{R^2 + (X_L – X_C)^2}Z=R2+(XL
Exemple de calcul :
Donné : R = 10Ω, X<sub>L</sub> = 15Ω, X<sub>C</sub> = 5Ω.
Calculer :
Xtotal=XL−XC=15Ω−5Ω=10ΩX_{\text{total}} = X_L – X_C = 15Ω – 5Ω = 10ΩXtotal
Z=102+102=200=14.14ΩZ = \sqrt{10^2 + 10^2} = \sqrt{200} = 14.14ΩZ=102+102

Comment calculer l’impédance dans un circuit RC ?
Dans un circuit RC (résistance et condensateur), l’impédance est calculée comme suit :
Z=R2+XC2Z = \sqrt{R^2 + X_C^2}Z=R2+XC2
Exemple de calcul :
Donné : R = 10Ω, X<sub>C</sub> = 20Ω.
Calculer :
Z=102+202=500=22.36ΩZ = \sqrt{10^2 + 20^2} = \sqrt{500} = 22.36ΩZ=102+202
Impédance dans les circuits en série et parallèle
- Circuits en série : Dans un circuit en série, l’impédance totale est la somme des impédances individuelles :
Ztotal=Z1+Z2+⋯+ZnZ_{\text{total}} = Z_1 + Z_2 + \cdots + Z_nZtotal
- Circuits parallèles : Comme discuté précédemment, l’impédance totale dans un circuit parallèle est calculée en utilisant la formule réciproque :
1Ztotal=1Z1+1Z2+⋯+1Zn\frac{1}{Z_{\text{total}}} = \frac{1}{Z_1} + \frac{1}{Z_2} + \cdots + \frac{1}{Z_n}Ztotal
Comment calculer l’impédance d’un condensateur ?
L’impédance d’un condensateur dans un circuit AC est donnée par :
XC=1ωCX_C = \frac{1}{\omega C}XC
- ω=2πf\omega = 2\pi fω=2πf (fréquence angulaire)
- C est la capacité
Exemple de calcul :
Donné : f = 60Hz, C = 100μF.
Calculer :
ω=2π×60=377 rad/s\omega = 2\pi \times 60 = 377 \text{ rad/s}ω=2π×60=377 rad/s
XC=1377×100×10−6=26.5ΩX_C = \frac{1}{377 \times 100 \times 10^{-6}} = 26.5ΩXC
Résumé
Déterminer l’impédance dans un circuit implique de comprendre l’interaction entre la résistance et la réactance. En appliquant les formules et méthodes pertinentes, telles que la méthode I-V et le calcul de l’impédance pour les circuits en série et parallèle, vous pouvez déterminer avec précision l’impédance dans n’importe quel circuit. Ces connaissances sont essentielles pour optimiser les performances du circuit et garantir un fonctionnement fiable dans diverses applications.
Si vous avez des questions ou avez besoin de plus d’informations sur les technologies PCB, n’hésitez pas à laisser un commentaire ci-dessous. N’oubliez pas de partager cet article si vous l’avez trouvé utile et restez connecté pour plus d’informations sur le fascinant monde de l’électronique.



